Q. 2進数を10進数になおす方法は?
A. たとえば、1011 を10進数にするなら、8 + 2 + 1 = 11 のように計算してなおします。
10進数の表し方
2進数を10進数に表すためには、10進数がどのようにあらわされているかを復習すると理解しやすいです。
例えば、123 という数字について考えましょう。
普段、あまり意識することはないですが、これは
100 が 1 個
10 が 2 個
1 が 3 個
集まってできた数、というのを 123 のようにあらわしています。

それぞれの「1」「2」「3」という数は、それぞれ
「100」「10」「1」がいくつずつ含まれているかということを表しているといえますね。
2進数→10進数への変換
2進数の表し方も、10進数と同じです。
それを理解すれば、2進数→10進数への変換も自動的にできます。
例えば、1011 という数字について考えましょう。
10進数では、1の位から順に、
1の個数、10の個数、100の個数、1000の個数…
を表しているというのを、さっき確認しました。
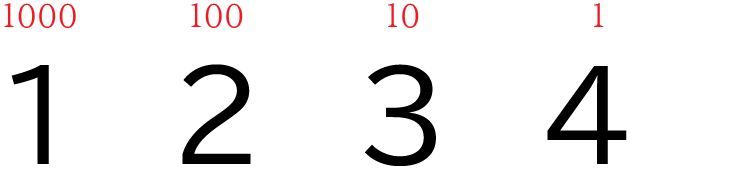
2進数では、1の位から順に、
1の個数、2の個数、4の個数、8の個数…
を表しています。
さらにケタが増えれば、16の個数、32の個数、64の個数…というように、2倍、2倍…と数が増えていきます。

なので、1011 の場合は、
8 が 1 個
4 が 0 個
2 が 1 個
1 が 1 個
集まった数だということです。
なので、計算すると
8 × 1 + 4 × 0 + 2 × 1 + 1 × 1 = 8 + 2 + 1 = 11
となります。
これがまさしく、1011 という2進数を、11という10進数に変換した、ということです。
数が大きくなっても、まったく同じように計算することができます。
例題1:11001
では、いま確認したことを使って、いくつか例題を解いてみましょう。
まずは 11001 という2進数を10進数になおします。
これは、
16 が 1 個
8 が 1 個
4 が 0 個
2 が 0 個
1 が 1 個
ということです。

つまり、これらを計算すると
16 × 1 + 8 × 1 + 4 × 0 + 2 × 0 + 1 × 1 = 16 + 8 + 1 = 25
よって、11001 という2進数を10進数に変換すると、25 となりました。
例題2:101111
つづいて、101111 という数字を10進数になおしましょう。
一番上(6ケタ目)の数字は何の個数を表しているかというと、
1, 2, 4, 8, 16, 32 と数えて、
「32 の個数」ということがわかります。
なので、101111 は
32 が 1 個
16 が 0 個
8 が 1 個
4 が 1 個
2 が 1 個
1 が 1 個
ということです。

あとはこれを計算します。
32 × 1 + 16 × 0 + 8 × 1 + 4 × 1 + 2 × 1 + 1 × 1 = 32 + 8 + 4 + 2 + 1 = 47
なので、101111 という2進数を10進数になおすと、47 になるということです。
例題3:10010000
最後は、もう少しはやく計算ができるように、一部を省略する方法を紹介します。
基本的な、やり方は同じです。
一番上の位は何の個数を表しているかというと、
1, 2, 4, 8, 16, 32, 64, 128
ということで、「128 の個数」を表しています。つまり、
128 が 1 個
16 が 1 個
ほかは 0 個
ということです。
ちなみに、10進数に変換するときに必要なのは、2進数で「1」となっている位だけなので、そこにだけ注目すればよいです。

計算すると、
128 + 16 = 144
となります。さきほどは「128 × 1」みたいに書いてましたが、×1 は書いても書かなくてもどちらでも同じなので、省略して書きました。
よって、10010000 を10進数になおすと、144 ということです。
まとめ
2進数を10進数に戻すさいは、
① それぞれのケタが「何の個数」なのかを確認して、
② 1となっているケタの数字をたし算していく
ことで変換できることを学習しました。
YouTube のほうでは、いま学んだことを 30 秒で復習できる動画をアップしていますので、ぜひ確認してみてください。




コメント